The boundedness of the small Hankel operator induced by an analytic symbol f and the Bergman projectionPvassociated tov,acting from the weighted Bergman space
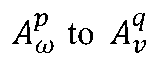 is characterized on the full range0 < p; q < ∞whenω , vbelong to the classDof radial weights admitting certain two-sided doubling conditions. Certain results obtained are equivalent to the boundedness of bilinear Hankel forms, which are in turn used to establish the weak factorization of the Bergman spaces.
is characterized on the full range0 < p; q < ∞whenω , vbelong to the classDof radial weights admitting certain two-sided doubling conditions. Certain results obtained are equivalent to the boundedness of bilinear Hankel forms, which are in turn used to establish the weak factorization of the Bergman spaces.











